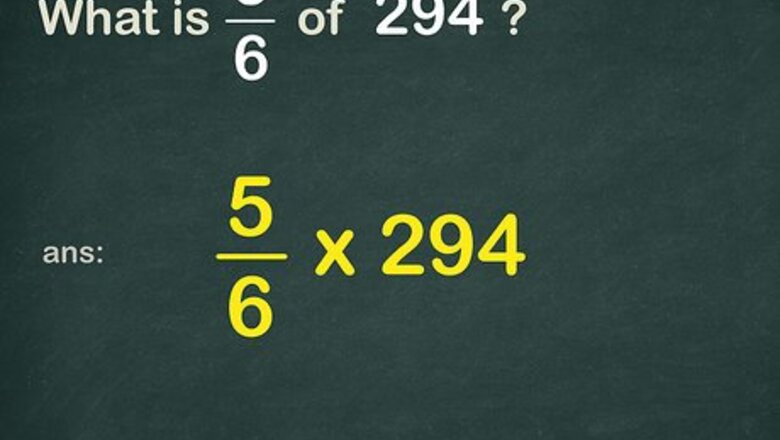
views
Calculating an Amount
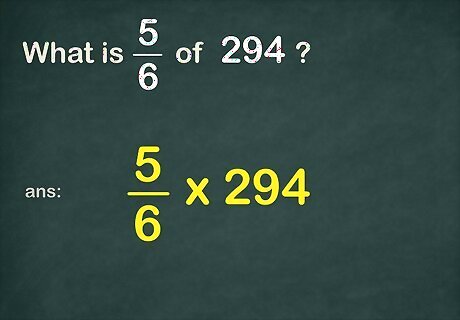
Set up the problem. When a problem asks you what a fraction of a whole number is, the problem is one of multiplication, and you need to multiply the fraction and the whole number. Look for the keyword of. When you see of in a word problem, you need to multiply. For example, if the problem asks, “What is 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of 294 {\displaystyle 294} 294," you need to set up 5 6 × 294 {\displaystyle {\frac {5}{6}}\times 294} {\frac {5}{6}}\times 294.
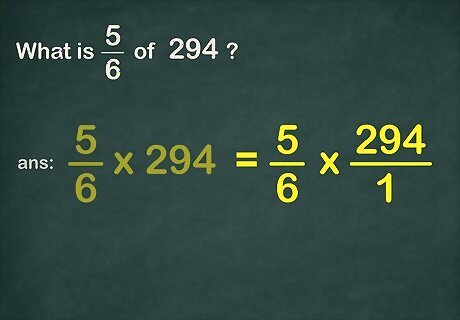
Turn the whole number into a fraction. To do this, give it a denominator of 1. Remember, the denominator is the number underneath the fraction bar. For example, you would change 294 {\displaystyle 294} 294 to 294 1 {\displaystyle {\frac {294}{1}}} {\frac {294}{1}}. So the new problem becomes 5 6 × 294 1 {\displaystyle {\frac {5}{6}}\times {\frac {294}{1}}} {\frac {5}{6}}\times {\frac {294}{1}}.
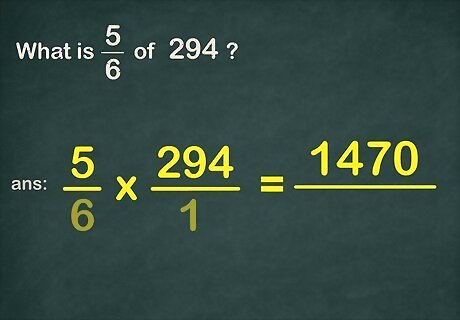
Multiply the numerators. Remember that the numerators are the numbers above the fraction bars. For example, 5 × 294 = 1 , 470 {\displaystyle 5\times 294=1,470} 5\times 294=1,470.
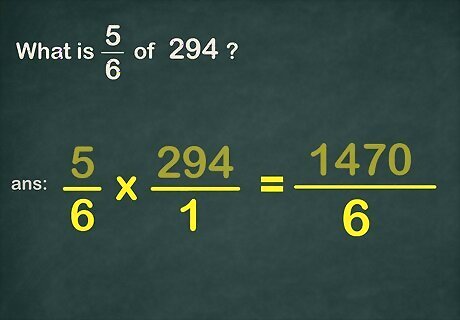
Multiply the denominators. Place this number under the product of the numerators. For example, 6 × 1 = 6 {\displaystyle 6\times 1=6} 6\times 1=6, so 5 6 × 294 1 = 1 , 470 6 {\displaystyle {\frac {5}{6}}\times {\frac {294}{1}}={\frac {1,470}{6}}} {\frac {5}{6}}\times {\frac {294}{1}}={\frac {1,470}{6}}.
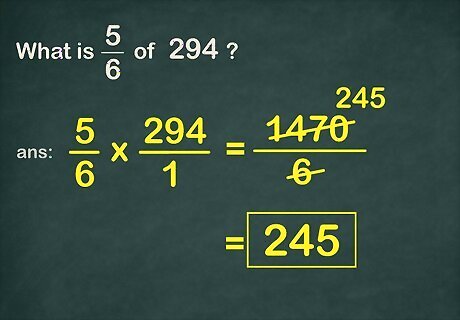
Simplify the fraction. To do this, divide the numerator by the denominator. This will give you your final answer as a whole number or in decimal form. If the result is not a whole number and you need the answer written in the form of a fraction, you should reduce the fraction by dividing the numerator and denominator by their greatest common factor. For complete instructions on how to reduce a fraction, read Reduce Fractions.https://www.bbc.co.uk/bitesize/topics/zsxhfg8/articles/z33csrd For example, 1 , 470 ÷ 6 = 245 {\displaystyle 1,470\div 6=245} 1,470\div 6=245, so 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of 294 = 245 {\displaystyle 294=245} 294=245. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To simplify fractions, you can divide both the numerator and denominator by a common factor. This creates a new, easier-to-use fraction with smaller components, but it represents the same value. For instance, if you divide both the numerator and denominator of 6/12 by 2, you get 3/6, which is equal to 1/2.
Calculating a Fraction

Understand what the problem is asking. When a problem asks you what fraction one whole number is of another whole number, you need to create a fraction and reduce it. Look for the key phrases “fraction of” or “out of.” For example, if the problem asks, “What fraction of 294 {\displaystyle 294} 294 is 245 {\displaystyle 245} 245,” you need to create a fraction from the two given whole numbers.

Determine the numerator and denominator. The numerator is the fraction of the whole. Often this will be the smaller number, but not always, so read the problem carefully. The denominator is the “complete” number. Look for the key phrase “fraction of x {\displaystyle x} x.” The x {\displaystyle x} x variable will be the denominator. For example, if the problem asks, “What fraction of 294 {\displaystyle 294} 294 is 245 {\displaystyle 245} 245,” you know that 245 {\displaystyle 245} 245 is the numerator, because this is the number that is a part, or fraction, of 294 {\displaystyle 294} 294. So the fraction is 245 294 {\displaystyle {\frac {245}{294}}} {\frac {245}{294}}.

Simplify the fraction. To do this, find the greatest factor that is common to the numerator and the denominator, then divide each by that factor. For complete instructions on how to reduce fractions, read Reduce Fractions. For example, the greatest common factor of 245 {\displaystyle 245} 245 and 294 {\displaystyle 294} 294 is 49 {\displaystyle 49} 49: 245 ÷ 49 = 5 {\displaystyle 245\div 49=5} 245\div 49=5, so the reduced numerator is 5 {\displaystyle 5} 5. 294 ÷ 49 = 6 {\displaystyle 294\div 49=6} 294\div 49=6, so the reduced denominator is 6 {\displaystyle 6} 6.So, 245 {\displaystyle 245} 245 is 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of 294 {\displaystyle 294} 294.
Changing an Amount By a Fraction

Understand what the problem is asking. If the problem is asking you to determine how much of something is left, or to decrease an amount, or to find a discount, you will first multiply to find the fractional amount, then subtract the fractional amount from the original whole number. If the problem is asking you to determine how much of something there is after an increase, you will first multiply to find the fractional amount, then add the fractional amount to the original whole number. For example, a problem might ask, “If you have $ 294 {\displaystyle \$294} \$294, and you give 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of it away, how much money do you have left?” In this case, you will multiply, then subtract. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Think about fractions as portions of a whole. Imagine dividing objects like pizzas or cakes into equal parts. Visualizing fractions this way improves comprehension, compared to relying solely on memorization. This approach can be helpful when adding, subtracting, and comparing fractions.
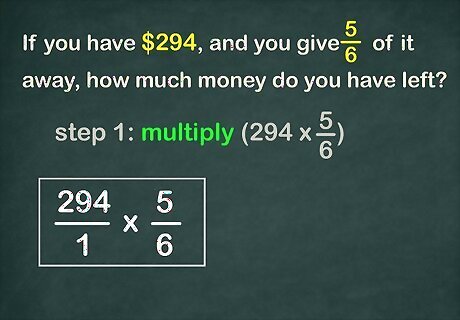
Set up the multiplication problem. To do this, turn the whole number into a fraction by placing it over a denominator of 1 {\displaystyle 1} 1. For example, to find 294 × 5 6 {\displaystyle 294\times {\frac {5}{6}}} 294\times {\frac {5}{6}}, you would change the problem to 294 1 × 5 6 {\displaystyle {\frac {294}{1}}\times {\frac {5}{6}}} {\frac {294}{1}}\times {\frac {5}{6}}.
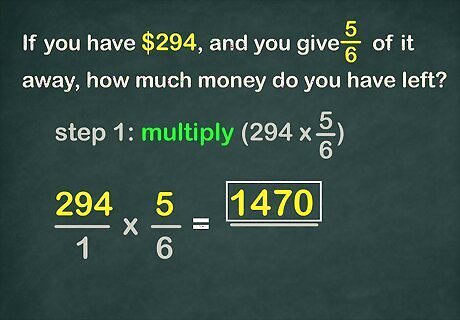
Multiply the numerators. This will give you your new numerator. For example, 294 × 5 = 1 , 470 {\displaystyle 294\times 5=1,470} 294\times 5=1,470.
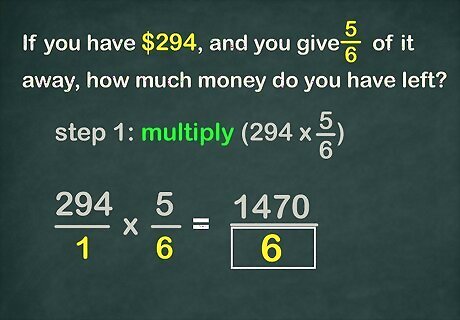
Multiply the denominators. This will give you your new denominator. Rewrite the new fraction. For example, 1 × 6 = 6 {\displaystyle 1\times 6=6} 1\times 6=6. So the new fraction is 1 , 470 6 {\displaystyle {\frac {1,470}{6}}} {\frac {1,470}{6}}.

Simplify the fraction. First divide the numerator by the denominator to see if the result is a whole number. If the result is not a whole number, you should reduce the fraction by dividing the numerator and denominator by their greatest common factor. For complete instructions on how to reduce a fraction, read Reduce Fractions. For example, 1 , 470 ÷ 6 = 245 {\displaystyle 1,470\div 6=245} 1,470\div 6=245, so 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of 294 = 245 {\displaystyle 294=245} 294=245. This is the fractional amount you are decreasing by.

Change the original amount by adding or subtracting the fractional amount. This will give you your final answer. For example, 294 − 245 = 49 {\displaystyle 294-245=49} 294-245=49. So, if you have $ 294 {\displaystyle \$294} \$294, and you give 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}} of it away, you have $ 49 {\displaystyle \$49} \$49 left.


















Comments
0 comment