views
- A magic square is a square grid of numbers where each row, column, and diagonal add up to the same total.
- Find the “magic constant” sum of each row, column, and diagonal with where n is the number of squares in each row.
- Use a solving technique based on the size of the magic square and how many boxes are in each row or column.
What is a magic square?
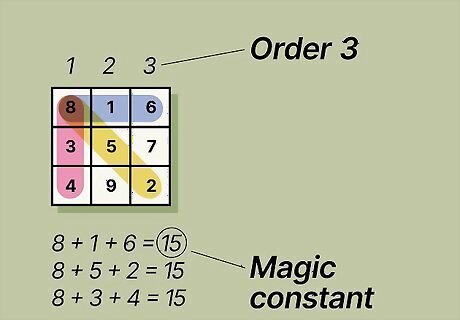
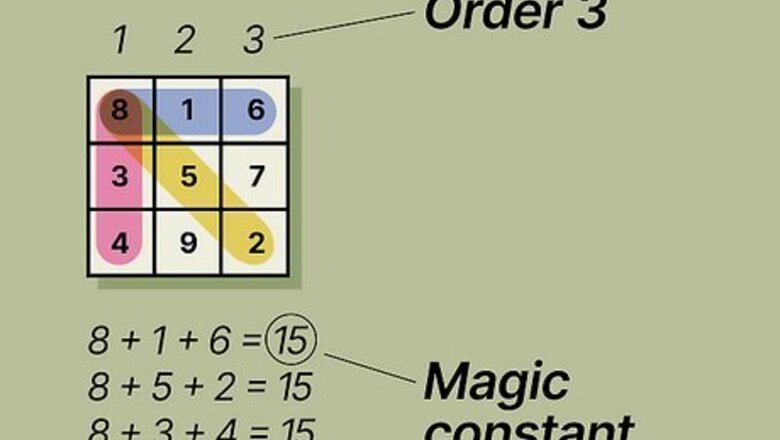
Magic squares have rows, columns, and diagonals that total the same sum. Each number in a magic square fits into a cell on a grid. The number of rows or columns determines the order, so an “order 3” magic square is one with a 3 x 3 grid. When you add up the numbers in a column, the value is called the “magic constant,” and all the other columns, rows, and diagonals will add up to that number. A normal magic square has consecutive numbers from 1 to n 2 {\displaystyle n^{2}} {\displaystyle n^{2}} (where n equals the order). A normal order 3 magic square with a magic constant of 15 would be:8 – 1 – 63 – 5 – 74 – 9 – 2 On a non-normal magic square, the lowest number may be higher than 1. A non-normal order 4 magic square with a magic constant of 87 could be:21 – 24 – 28 – 1427 – 15 – 20 – 2516 – 30 – 22 – 1923 – 18 – 17 – 29
3 x 3 or Odd-Numbered Squares

Calculate the magic constant. To find the magic constant (S) for a normal magic square use the formula S = n [ ( n 2 + 1 ) / 2 ] {\displaystyle S=n[(n^{2}+1)/2]} {\displaystyle S=n[(n^{2}+1)/2]} where n {\displaystyle n} n equals the order, or number of rows, in the magic square. So for a 3×3 magic square, the formula would be: S = 3 [ ( 3 2 + 1 ) / 2 ] {\displaystyle 3[(3^{2}+1)/2]} {\displaystyle 3[(3^{2}+1)/2]} S = 3 [ ( 9 + 1 ) / 2 ] {\displaystyle 3[(9+1)/2]} {\displaystyle 3[(9+1)/2]} S = 3 ( 10 / 2 ) {\displaystyle 3(10/2)} {\displaystyle 3(10/2)} S = 3 ( 5 ) {\displaystyle 3(5)} {\displaystyle 3(5)} S = 15 All rows, columns, and diagonals must add up to 15. Normal magic squares always have the same magic constant. If solving for a non-normal square, add all the numbers together and divide by the number of rows to find the magic constant.
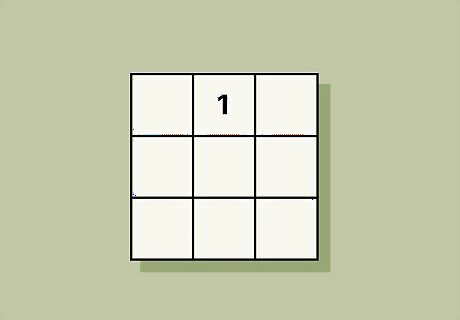
Place the number 1 in the center box on the top row. The placement is the same for any normal magic square with an odd number of columns or rows. Find the center square in the top row and write down the number 1 to get started. Example: If you have a 3 x 3 magic square, put 1 in the second box in the top row. Example: For a 15 x 15 magic square, put the 1 in the eighth box of the row.
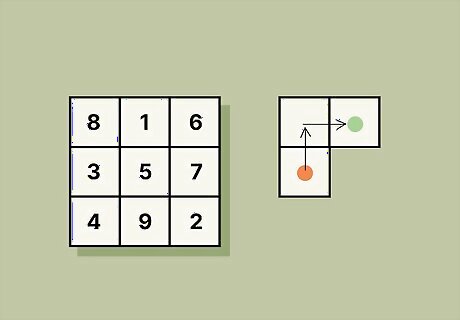
Follow an up-one, right-one pattern to fill in the remaining numbers. Start at the middle box in the top row where you placed the 1. Move up one row and to the right one column and write in the next number sequentially. Whenever a move takes you above the top row (like the first move will), go to the bottom row instead. If you need to move a square to the right but are already in the rightmost column, move to the leftmost column instead. Continue filling in the square following the pattern until it’s complete. Example: In a normal 3 x 3 square, the 2 goes in the bottom right corner and the 3 goes in the left column in the center row. If the movement takes you to a box that is already occupied, go back to the last box that has been filled in, and place the next number directly below it. For example, when you place the 4 in a 3 x 3 magic square, it fits in the bottom left corner below the 3. Then, following the same up-one, right-one pattern, place the 5 in the center of the puzzle to continue.
4 x4 or Doubly Even Magic Square
Recognize a doubly even square if the sides are divisible by 4. Count the number of squares in a single row or column of your magic square. If the magic square is an order 4 square or the number is evenly divisible by 4 (8, 12, 16, etc.), then you’re working with a doubly even square.
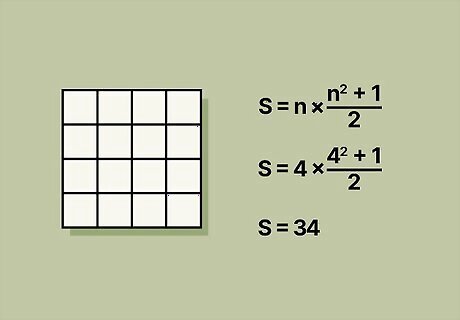
Calculate the magic constant. Use the formula S = [ n ( n 2 + 1 ) ] / 2 {\displaystyle S=[n(n^{2}+1)]/2} {\displaystyle S=[n(n^{2}+1)]/2}, where n {\displaystyle n} n equals the order, or the number of boxes per row in your magic square. So, for a 4 x 4 square, the magic constant calculation becomes: S = [ 4 ( 4 2 + 1 ) ] / 2 {\displaystyle [4(4^{2}+1)]/2} {\displaystyle [4(4^{2}+1)]/2} S = [ 4 ( 16 + 1 ) ] / 2 {\displaystyle [4(16+1)]/2} {\displaystyle [4(16+1)]/2} S = ( 4 ( 17 ) ) / 2 {\displaystyle (4(17))/2} {\displaystyle (4(17))/2} S = 68 / 2 {\displaystyle 68/2} {\displaystyle 68/2} S = 34 All rows, columns, and diagonals must add up to 34.
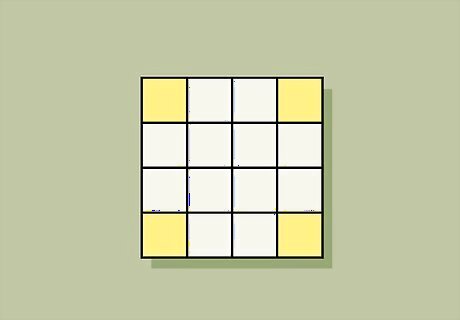
Create Highlights A–D in the corners of the magic square. Form a mini square in each corner that has a length of n / 4 {\displaystyle n/4} n/4 on each side, where n {\displaystyle n} n is the magic square’s order. Start in the top left corner and label the mini squares A, B, C, and D going clockwise around the magic square. In a 4 x 4 square, only mark the 4 corner boxes as your highlights. For an 8 x 8 magic square, the Highlights become 2 x 2 mini squares in the corners. In a 12 x 12 square, each Highlight is a 3 x 3 area.

Create the Central Highlight. Mark all the boxes in the center of the magic square in a square area of length n / 2 {\displaystyle n/2} {\displaystyle n/2}, where n {\displaystyle n} n is the magic square’s order. The Central highlight will touch a 1 corner each from Highlights A–D, but it shouldn’t overlap them at all. In a 4 x 4 square, the Central Highlight would be a 2 x 2 area in the center. In an 8 x 8 square, the Central Highlight would be a 4 x 4 area in the center.
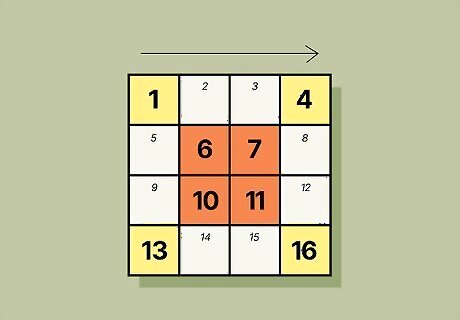
Fill in the highlighted areas of your magic square. Start in the top left corner of your magic square. Place 1 in the top left corner and count the boxes across the top row. If a box is highlighted, fill it in with the number. Work down the entire magic square until all the highlighted areas are filled in. In an order 4 magic square, the boxes and their numbers are: 1 in the top-left box and 4 in the top-right box 6 and 7 in the second and third boxes in Row 2 10 and 11 in the second and third boxes of Row 3 13 in the bottom-left box and 16 in the bottom-right box
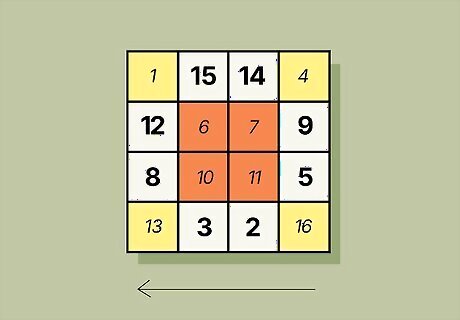
Fill in the rest of the magic square by counting backward. Begin again with the top left box, but skip over all the boxes that you already filled in. Count down from the highest number in the magic square as you work across the row, and add the number to any empty box. Once you finish, your magic square is complete. In a 4x4 magic square, the boxes you fill in are: 15 and 14 in the second and third boxes in Row 1 12 in the leftmost box and 9 in the rightmost box in Row 2 8 in the leftmost box and 5 in the rightmost box in Row 3 3 and 2 in the second and third boxes in Row 4
Singly Even Magic Square
Check if the square’s sides are divisible by 2, but not 4. Singly even magic squares have an even number of boxes in their rows and columns. If you divide the magic square’s order by 2 and get an odd number as the result, you’re working with a singly even square. The smallest possible singly even magic square is 6 x 6 since 2 x 2 magic squares are impossible to make.
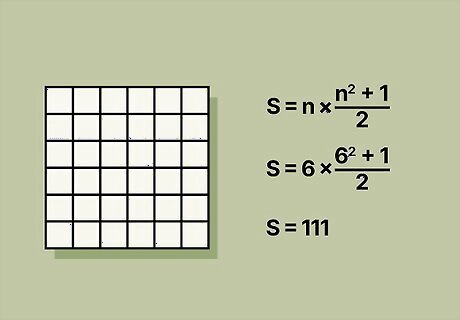
Calculate the magic constant. Use the formula S = [ n ( n 2 + 1 ) ] / 2 {\displaystyle S=[n(n^{2}+1)]/2} {\displaystyle S=[n(n^{2}+1)]/2}, where n equals the magic square’s order, or the number of boxes per side. For a 6 x 6 square, your formula would look like: S = [ 6 ( 6 2 + 1 ) ] / 2 {\displaystyle [6(6^{2}+1)]/2} {\displaystyle [6(6^{2}+1)]/2} S = [ 6 ( 36 + 1 ) ] / 2 {\displaystyle [6(36+1)]/2} {\displaystyle [6(36+1)]/2} S = ( 6 ( 37 ) ) / 2 {\displaystyle (6(37))/2} {\displaystyle (6(37))/2} S = 222 / 2 {\displaystyle 222/2} {\displaystyle 222/2} S = 111 Hence, the magic constant for a 6×6 square is 111 and all rows, columns, and diagonals will add up to this number.

Divide the magic square into four quadrants of equal size. Divide the magic square’s order by 2 to find out how many boxes each side of the quadrant should be. Draw lines to separate the quadrants and label them A (top left), C (top right), D (bottom left), and B (bottom right). For a 6 x 6 square, each quadrant is 3 x 3 boxes.
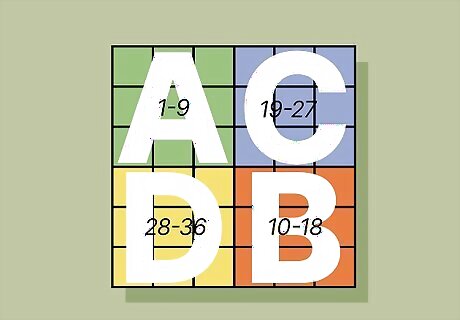
Assign each quadrant a number range. Count the number of boxes in a single quadrant to know how many numbers are in each section. Assign Quadrant A the first quarter of numbers, Quadrant B the second quarter, Quadrant C the third quarter, and Quadrant D the final quarter. That way, you know which numbers are going into specific quadrants without accidentally reusing them. In a 6 x 6 square, Quadrant A contains the numbers 1-9, Quadrant B has 10-18, Quadrant C has 19-27, and Quadrant D ends with 28-36.
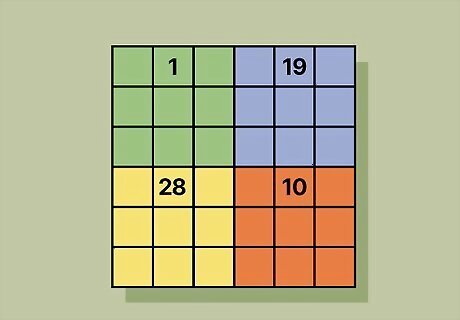
Solve each quadrant using a one-up, one-right pattern. In each quadrant, put the lowest value in the center box in the top row. Move up one row and to the right one column to place your next number. If you go above the top row of the quadrant, then move to the bottom row instead. When you go past the rightmost column, add the number to the leftmost column. If there’s already a number in the next square, put the next number directly below the last one.
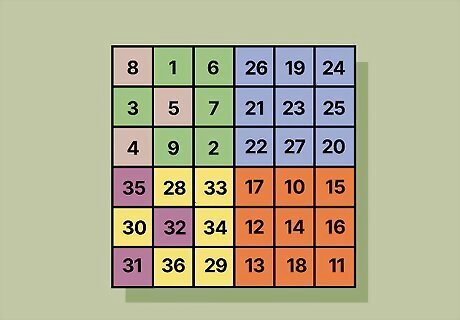
Create Highlights A and D. In Quadrant A, mark all the squares in the top row to the left of the quadrant’s center square. In the second row, skip the first column and highlight the center square and remaining boxes to the left of it. Then, mark the squares in the bottom row that share a column with the boxes in the top row to finish the A highlights. Then, repeat the same process in Quadrant D for the D highlights. In a 6 x 6 square, Highlight A-1 is the top right box, Highlight A-2 is the center box in the middle row, and Highlight A-3 is the bottom right corner of Quadrant A. The D highlights are in the same position in Quadrant D. If you tried to add up your columns, rows, and diagonals right now, the square isn’t considered magic since they don’t add up to the same magic constant yet.
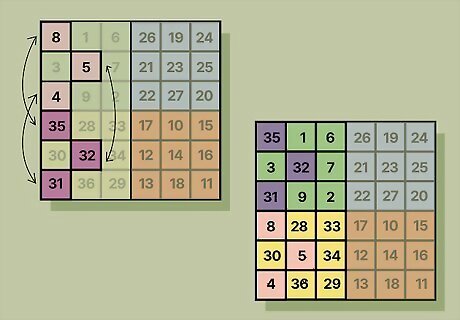
Swap the positions of Highlights A and D. Simply take the number from one square and swap it with the corresponding box between Quadrant A and Quadrant D. Once you’ve done this, all the rows, columns, and diagonals in a 6 x 6 magic square will add up to the magic constant you calculated. Example: In a 6 x 6 magic square, 8 swaps positions with 35, 5 swaps with 32, and 4 swaps with 31.
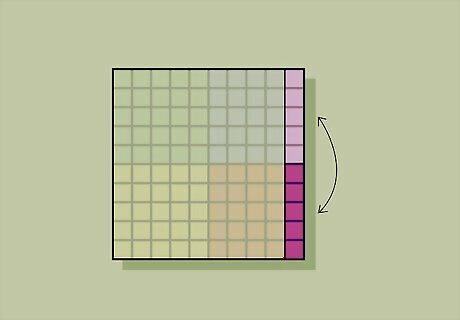
Swap the right columns in B and C for magic squares larger than 6 x 6. Count the highlighted columns in the top row of Quadrant A and subtract 1. Count that number of columns in from the right side of Quadrants B and C and highlight all the squares. Move the values in Quadrant C into the corresponding squares in Quadrant B, and vice-versa to complete your magic square. For a 10 x 10 magic square, only swap the rightmost column in quadrants B and C. For a 14 x 14 magic square, swap the 2 rightmost columns instead.


![{\displaystyle S=n[(n^{2}+1)/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6645cd02ee35be03b0fc03e0e9c3dd8b3295d96)















Comments
0 comment