views
K
a
{\displaystyle K_{a}}
)—the acid dissociation constant—tells you the strength of an acid in a different and more specific way than the better-known pH. Because Ka produces extremely wide-ranging values, pKa (
p
K
a
{\displaystyle pK_{a}}
)—the negative logarithm (base 10) of Ka—is often used to simplify the range of acid strength values. If all of this is twisting your brain a little, here’s some good news: it’s actually pretty easy to figure out Ka from pKa (or pKa from Ka) with a scientific calculator, or to get a decent estimate without a calculator. And we’ll show you how to do it all!
- Calculate Ka from pKa with the equation .
- Calculate pKa from Ka with the equation .
- Estimate pKa from Ka (or vice versa) based on the pseudo-equation .
Calculating Ka from pKa
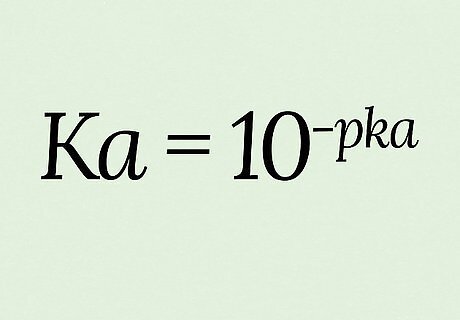
Use the equation K a = 10 − p K a {\displaystyle Ka=10^{-pKa}} {\displaystyle Ka=10^{-pKa}} for this conversion. pKa is defined as the negative logarithm (-log) of Ka, which means you calculate pKa with the calculation p K a = − l o g ( K a ) {\displaystyle pKa=-log(Ka)} {\displaystyle pKa=-log(Ka)}. Solving instead for Ka requires you to raise both sides of the equation by exponents of 10: 10 p K a = 10 − l o g ( K a ) {\displaystyle 10^{pKa}=10^{-log(Ka)}} {\displaystyle 10^{pKa}=10^{-log(Ka)}} 10 − p K a = 10 l o g ( K a ) {\displaystyle 10^{-pKa}=10^{log(Ka)}} {\displaystyle 10^{-pKa}=10^{log(Ka)}} 10 − p K a = K a {\displaystyle 10^{-pKa}=Ka} {\displaystyle 10^{-pKa}=Ka} → K a = 10 − p k a {\displaystyle Ka=10^{-pka}} {\displaystyle Ka=10^{-pka}} For this example, we’ll say p K a = 14 {\displaystyle pKa=14} {\displaystyle pKa=14} (which is in fact the pKa for plain water).
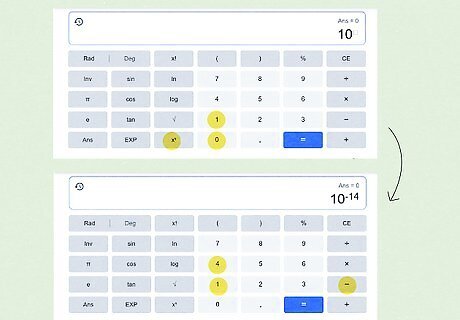
Enter the right side of the equation in your scientific calculator. Using a scientific calculator varies a bit by model and type (for both online and physical calculators), but the buttons are generally similar. For this article, we’ll use the online scientific calculator that appears when you Google “scientific calculator.” Type in 10 {\displaystyle 10} 10. Press the x y {\displaystyle x^{y}} {\displaystyle x^{y}} button. Type − 14 {\displaystyle -14} {\displaystyle -14} in the superscript box. Press the = {\displaystyle =} = button.

Translate the answer 1 e − 14 {\displaystyle 1e-14} {\displaystyle 1e-14}. The result you get may not appear in the format you expect, but it is the right answer. Simply substitute ∗ 10 {\displaystyle *10} {\displaystyle *10} for e {\displaystyle e} e and raise − 14 {\displaystyle -14} {\displaystyle -14} to superscript: 1 e − 14 {\displaystyle 1e-14} {\displaystyle 1e-14} equals 1 ∗ 10 − 14 {\displaystyle 1*10^{-14}} {\displaystyle 1*10^{-14}}. So a pKa of 14 {\displaystyle 14} 14 equals a Ka of 1 ∗ 10 − 14 {\displaystyle 1*10^{-14}} {\displaystyle 1*10^{-14}}. In some cases, your calculator may provide the answer in decimal form, such as K a = 0.00072 {\displaystyle Ka=0.00072} {\displaystyle Ka=0.00072} instead of its equivalent K a = 7.2 ∗ 10 − 4 {\displaystyle Ka=7.2*10^{-4}} {\displaystyle Ka=7.2*10^{-4}}. The latter format is typically how Ka is represented, however.
Calculating pKa from Ka

Do this conversion with the equation p K a = − l o g ( K a ) {\displaystyle pKa=-log(Ka)} {\displaystyle pKa=-log(Ka)}. pKa exists largely as a matter of convenience, since the Ka of acids are unwieldy values like 1.54 ∗ 10 − 2 {\displaystyle 1.54*10^{-2}} {\displaystyle 1.54*10^{-2}} and 1.34 ∗ 10 − 5 {\displaystyle 1.34*10^{-5}} {\displaystyle 1.34*10^{-5}}. However, converting to the negative logarithm (-log) of these values creates much more manageable figures like 1.81 {\displaystyle 1.81} {\displaystyle 1.81} and 4.87 {\displaystyle 4.87} {\displaystyle 4.87}. Converting to the -log means that a lower pKa value indicates a stronger acid, as opposed to the Ka, in which a higher Ka value indicates a stronger acid. In this example, let’s make K a = 4 ∗ 10 − 4 {\displaystyle Ka=4*10^{-4}} {\displaystyle Ka=4*10^{-4}} (nitrous acid).

Input the right side of the equation in a scientific calculator. As with our pKa to Ka conversion, we’ll assume you’re using Google search’s scientific calculator: Press the − {\displaystyle -} - button. Press the l o g {\displaystyle log} {\displaystyle log} button. Enter 4 ∗ 10 {\displaystyle 4*10} {\displaystyle 4*10} inside the parentheses. Press the x y {\displaystyle x^{y}} {\displaystyle x^{y}} button. Enter − 4 {\displaystyle -4} -4 in the superscript box. Press the = {\displaystyle =} = button.
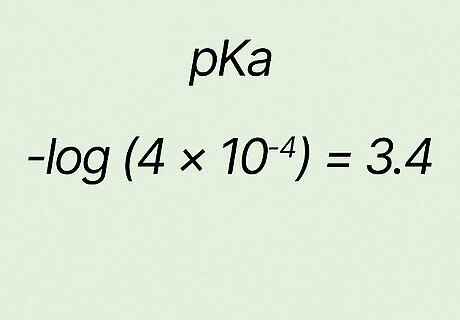
Confirm your answer. For the example − l o g ( 4 ∗ 10 − 4 ) {\displaystyle -log(4*10^{-4})} {\displaystyle -log(4*10^{-4})}, your answer should be 3.4 {\displaystyle 3.4} {\displaystyle 3.4}. So in this case p K a = 3.4 {\displaystyle pKa=3.4} {\displaystyle pKa=3.4}.
Can I find Ka (or pKa) without a calculator?
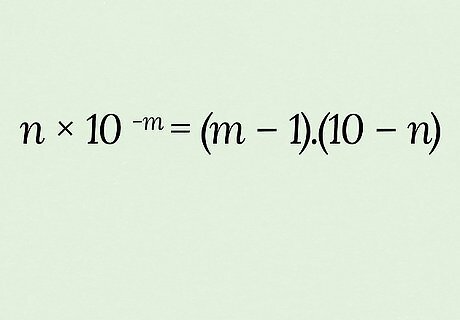
You can get a quick estimate that may help on a multiple-choice exam. The trick is to use the “equation” n ∗ 10 − m = ( m − 1 ) . ( 10 − n ) {\displaystyle n*10^{-m}=(m-1).(10-n)} {\displaystyle n*10^{-m}=(m-1).(10-n)}: Finding an estimate of pKa from Ka is easier. Say, for example, Ka equals 2.33 ∗ 10 − 11 {\displaystyle 2.33*10^{-11}} {\displaystyle 2.33*10^{-11}}: Based on this Ka and the “equation” given above, n = 2.33 {\displaystyle n=2.33} {\displaystyle n=2.33} and m = 11 {\displaystyle m=11} {\displaystyle m=11}. Round n {\displaystyle n} n to a single digit if needed (2 in this case), then plug these into the second half of the “equation.” ( 11 − 1 ) . ( 10 − 2 ) {\displaystyle (11-1).(10-2)} {\displaystyle (11-1).(10-2)} → 10.8 {\displaystyle 10.8} {\displaystyle 10.8}. Your estimate of Ka is 10.8, while the actual answer is 10.63. Estimating Ka from pKa (let’s say it equals 10.63) is a bit trickier and less accurate: Round to a single digit after the decimal as needed: 10.63 → 10.7 Based on the ( m − 1 ) . ( 10 − n ) {\displaystyle (m-1).(10-n)} {\displaystyle (m-1).(10-n)} half of the “equation,” add 1 to the 10 (from 10.7) to get m {\displaystyle m} m and subtract the 7 (from 10.7) from 10 to get n {\displaystyle n} n; so m = 11 {\displaystyle m=11} {\displaystyle m=11} and n = 3 {\displaystyle n=3} {\displaystyle n=3}. Plug the results (m=11 & n=3) into the first half of the “equation”: 3 ∗ 10 − 11 {\displaystyle 3*10^{-11}} {\displaystyle 3*10^{-11}} is your estimate for Ka, while the actual answer is 2.33 ∗ 10 − 11 {\displaystyle 2.33*10^{-11}} {\displaystyle 2.33*10^{-11}}.
Sample Problems
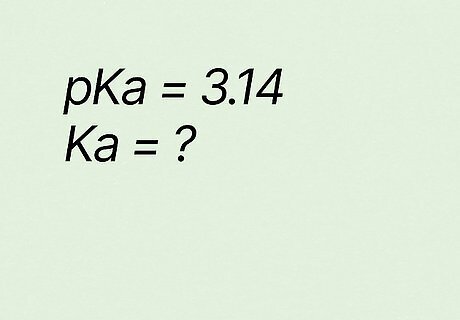
What is Ka if pKa equals 3.14? K a = 10 − p K a {\displaystyle Ka=10^{-pKa}} {\displaystyle Ka=10^{-pKa}} K a = 10 − 3.14 {\displaystyle Ka=10^{-3.14}} {\displaystyle Ka=10^{-3.14}} K a = 0.00072 {\displaystyle Ka=0.00072} {\displaystyle Ka=0.00072} → K a = 7.2 ∗ 10 − 4 {\displaystyle Ka=7.2*10^{-4}} {\displaystyle Ka=7.2*10^{-4}}
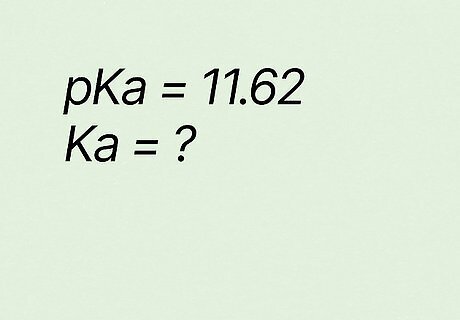
What is Ka if pKa equals 11.62? K a = 10 − p K a {\displaystyle Ka=10^{-pKa}} {\displaystyle Ka=10^{-pKa}} K a = 10 − 11.65 {\displaystyle Ka=10^{-11.65}} {\displaystyle Ka=10^{-11.65}} K a = 2.2 e − 12 {\displaystyle Ka=2.2e^{-12}} {\displaystyle Ka=2.2e^{-12}} → K a = 2.2 ∗ 10 − 12 {\displaystyle Ka=2.2*10^{-12}} {\displaystyle Ka=2.2*10^{-12}}
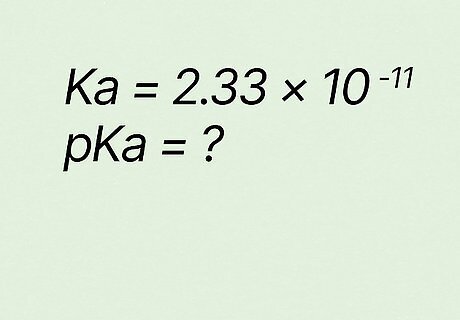
What is pKa if Ka equals 2.33 ∗ 10 − 11 {\displaystyle 2.33*10^{-11}} {\displaystyle 2.33*10^{-11}}? p K a = − l o g ( K a ) {\displaystyle pKa=-log(Ka)} {\displaystyle pKa=-log(Ka)} p K a = − l o g ( 2.33 ∗ 10 − 11 ) {\displaystyle pKa=-log(2.33*10^{-11})} {\displaystyle pKa=-log(2.33*10^{-11})} p K a = 10.63 {\displaystyle pKa=10.63} {\displaystyle pKa=10.63}
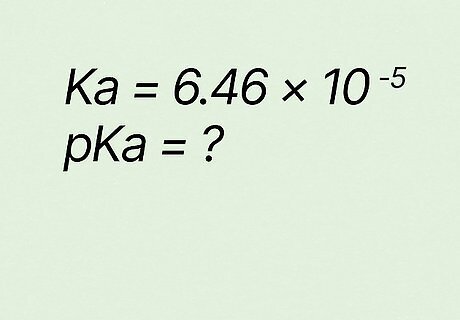
What is pKa if Ka equals 6.46 ∗ 10 − 5 {\displaystyle 6.46*10^{-5}} {\displaystyle 6.46*10^{-5}}? p K a = − l o g ( K a ) {\displaystyle pKa=-log(Ka)} {\displaystyle pKa=-log(Ka)} p K a = − l o g ( 6.46 ∗ 10 − 5 ) {\displaystyle pKa=-log(6.46*10^{-5})} {\displaystyle pKa=-log(6.46*10^{-5})} p K a = 4.19 {\displaystyle pKa=4.19} {\displaystyle pKa=4.19}
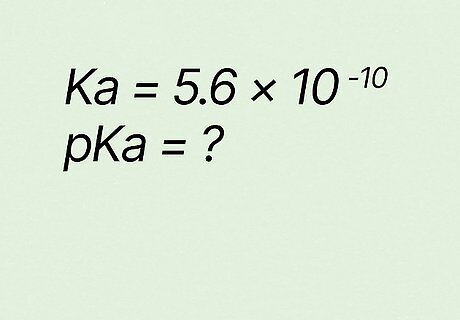
Estimate pKa if Ka equals 5.6 ∗ 10 − 10 {\displaystyle 5.6*10^{-10}} {\displaystyle 5.6*10^{-10}}. Using n ∗ 10 − m = ( m − 1 ) . ( 10 − n ) {\displaystyle n*10^{-m}=(m-1).(10-n)} {\displaystyle n*10^{-m}=(m-1).(10-n)}, plug 5 (from 5.6) in as n {\displaystyle n} n and 6 (from 5.6) in as m {\displaystyle m} m in the second half of the “equation.” (10-1).(10-6) → 9.4. The accurate result for PKa is 9.25.






















Comments
0 comment