views
X
Research source
These tables can still be useful for quickly calculating logarithms or multiplying large numbers, once you figure out how to use them.
Quick Instructions
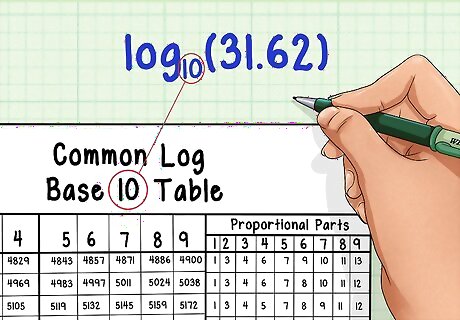
Choose the correct table. To find loga(n), you'll need a loga table. Most log tables are for base-10 logarithms, called "common logs." Example: log10(31.62) requires a base-10 table.
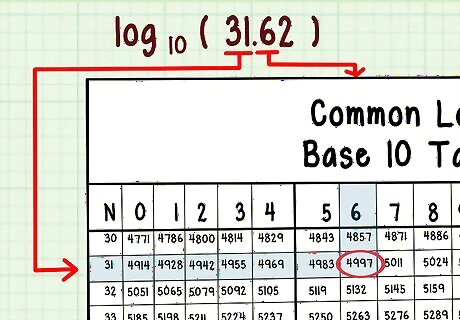
Find the correct cell. Look for the cell value at the following intersections, ignoring all decimal places: Row labeled with first two digits of n Column header with third digit of n Example: log10(31.62) → row 31, column 6 → cell value 0.4997.
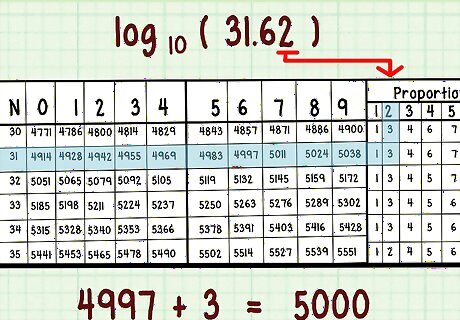
Use smaller chart for precise numbers. Some tables have a smaller set of columns on the right side of the chart. Use these to adjust answer if n has four or more significant digits: Stay in same row Find small column header with fourth digit of n Add this to previous value Example: log10(31.62) → row 31, small column 2 → cell value 2 → 4997 + 2 = 4999.

Prefix a decimal point. The log table only tells you the portion of your answer after the decimal point. This is called the "mantissa." Example: Solution so far is ?.4999
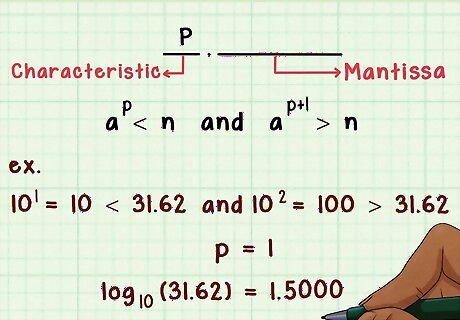
Find the integer portion. Also called the "characteristic". By trial and error, find integer value of p such that
a
p
<
n
{\displaystyle a^{p}
In-Depth Instructions
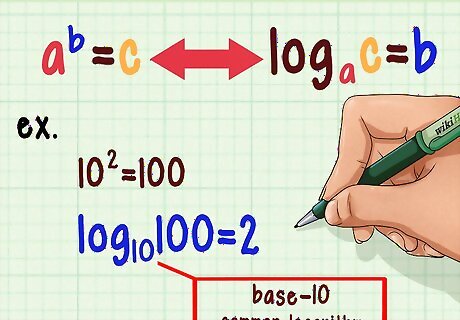
Understand what a logarithm is. 10 is 100. 10 is 1000. The powers 2 and 3 are the base-10 logarithms of 100 and 1000. In general, a = c can be rewritten as logac = b. So, saying "ten to the power of two is 100" is equivalent to saying "the base-ten log of 100 is two." Each logarithmic table is only usable with a certain base (a in the equation above). By far the most common type of log table uses base-10 logs, also called the common logarithm. Multiply two numbers by adding their powers. For example: 10 * 10 = 10, or 100 * 1000 = 100,000. The natural log, represented by "ln", is the base-e log, where e is the constant 2.718. This is a useful number in many areas of math and physics. You can use natural log tables in the same way that you use common, or base-10, log tables.

Identify the characteristic of the number whose log you want to find. Let's say you want to find the base-10 log of 15 on a common log table. 15 lies between 10 (10) and 100 (10), so its logarithm will lie between 1 and 2, or be 1.something. 150 lies between 100 (10) and 1000 (10), so its logarithm will lie between 2 and 3, or be 2.something. The .something is called the mantissa; this is what you will find in the log table. What comes before the decimal point (1 in the first example, 2 in the second) is the characteristic.
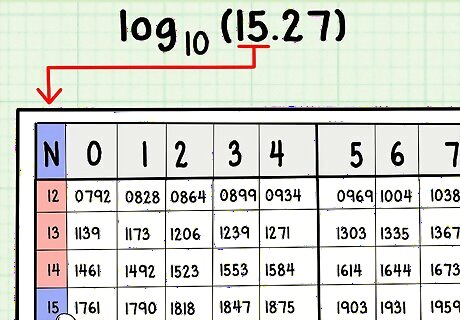
Slide your finger down to the appropriate row on the table using the leftmost column. This column will show the first two or, for some large log tables, three digits of the number whose logarithm you're looking up. If you're looking up the log of 15.27 in a normal log table, go to the row marked 15. If you're looking up the log of 2.57, go to the row marked 25. Sometimes the numbers in this row will have a decimal point, so you'll look up 2.5 rather than 25. You can ignore this decimal point, as it won't affect your answer. Also ignore any decimal points in the number whose logarithm you're looking up, as the mantissa for the log of 1.527 is no different from that of the log of 152.7.
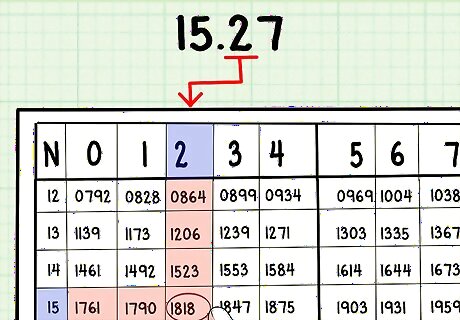
On the appropriate row, slide your finger over to the appropriate column. This column will be the one marked with the next digit of the number whose logarithm you're looking up. For example, if you want to find the log of 15.27, your finger will be on the row marked 15. Slide your finger along that row to the right to find column 2. You will be pointing at the number 1818. Write this down.
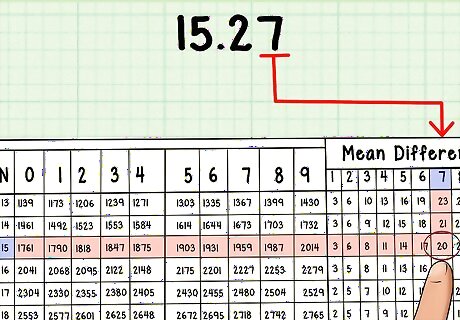
If your log table has a mean difference table, slide your finger over to the column in that table marked with the next digit of the number you're looking up. For 15.27, this number is 7. Your finger is currently on row 15 and column 2. Slide it over to row 15 and mean differences column 7. You will be pointing at the number 20. Write this down.

Add the numbers found in the two preceding steps together. For 15.27, you will get 1838. This is the mantissa of the logarithm of 15.27.

Add the characteristic. Since 15 is between 10 and 100 (10 and 10), the log of 15 must be between 1 and 2, so 1.something, so the characteristic is 1. Combine the characteristic with the mantissa to get your final answer. Find that the log of 15.27 is 1.1838.
Finding the Anti-Log
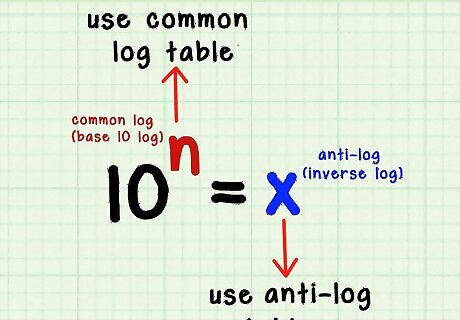
Understand the anti-log table. Use this when you have the log of a number but not the number itself. In the formula 10 = x, n is the common log, or base-ten log, of x. If you have x, find n using the log table. If you have n, find x using the anti-log table. The anti-log is also commonly known as the inverse log.
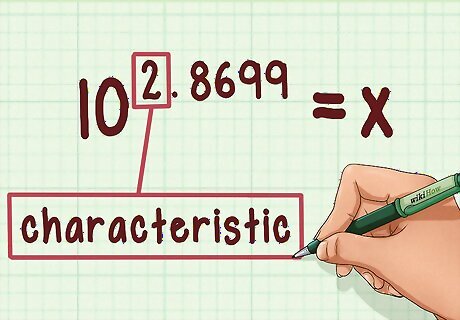
Write down the characteristic. This is the number before the decimal point. If you're looking up the anti-log of 2.8699, the characteristic is 2. Mentally remove it from the number you're looking up, but make sure to write it down so you don't forget it - it will be important later.
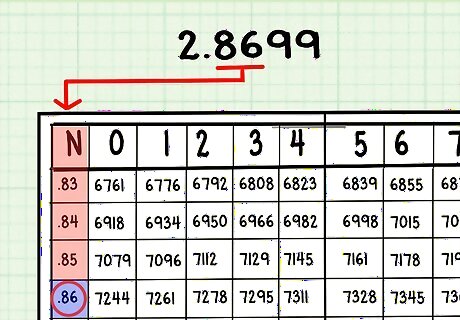
Find the row that matches the first part of the mantissa. In 2.8699, the mantissa is .8699. Most anti-log tables, like most log tables, have two digits in the leftmost column, so run your finger down that column until you find .86.
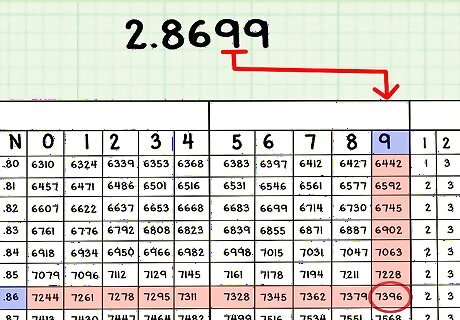
Slide your finger over to the column marked with the next digit of the mantissa. For 2.8699, slide your finger along the row marked .86 to find the intersection with column 9. This should read 7396. Write this down.
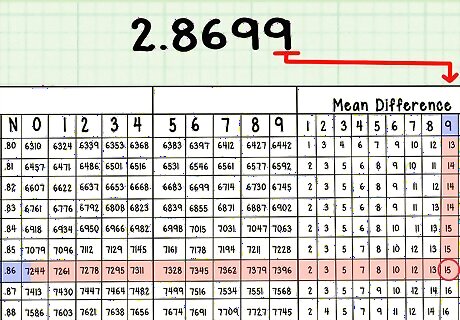
If your anti-log table has a table of mean differences, slide your finger over to the column in that table marked with the next digit of the mantissa. Make sure to keep your finger in the same row. In this case, you will slide your finger over to the last column in the table, column 9. The intersection of row .86 and mean differences column 9 is 15. Write that down.

Add the two numbers from the two previous steps. In our example, these are 7396 and 15. Add them together to get 7411.
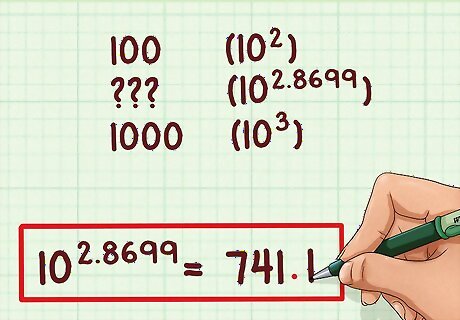
Use the characteristic to place the decimal point. Our characteristic was 2. This means that the answer is between 10 and 10, or between 100 and 1000. In order for the number 7411 to fall between 100 and 1000, the decimal point must go after three digits, so that the number is about 700 rather than 70, which is too small, or 7000, which is too big. So the final answer is 741.1.
Multiplying Numbers
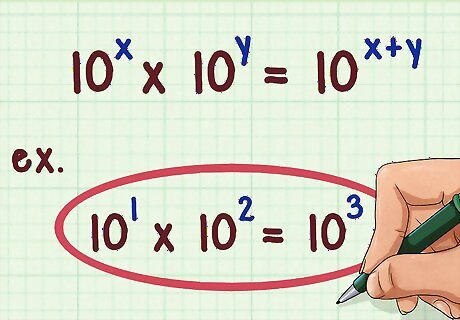
Understand how to multiply numbers using their logarithms. We know that 10 * 100 = 1000. Written in terms of powers (or logarithms), 10 * 10 = 10. We also know that 1 + 2 = 3. In general, 10 * 10 = 10. So, the sum of the logarithms of two different numbers is the logarithm of the product of those numbers. We can multiply two numbers of the same base by adding their powers.
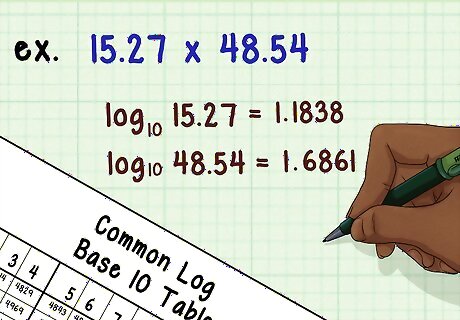
Look up the logarithms of the two numbers you want to multiply. Use the method above to find the logarithms. For example, if you want to multiply 15.27 and 48.54, you would find the log of 15.27 to be 1.1838 and the log of 48.54 to be 1.6861.

Add the two logarithms to find the logarithm of the solution. In this example, add 1.1838 and 1.6861 to get 2.8699. This number is the logarithm of your answer.
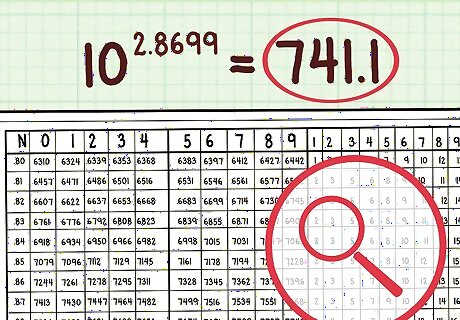
Look up the anti-logarithm of the result from the above step to find the solution. You can do this by finding the number in the body of the table closest to the mantissa of this number (8699). The more efficient and reliable method, however, is to find the answer in the table of anti-logarithms, as described in the method above. For this example, you will get 741.1.
















Comments
0 comment