
views
Simplifying Square Roots

Factor each radicand into prime numbers. An easy way to factor a number is by creating a factor tree diagram. Read Do a Factor Tree for complete instructions. A radicand is the number under the radical sign. A prime number is a number that can only be divided evenly by 1 and itself, for example, 2, 3, 5, 7, 11, etc. You do NOT need to factor any coefficients. A coefficient is a number in front of the radical sign. Let’s say, for example, that you want to add 20 + 4 45 + 5 + 7 . {\displaystyle {\sqrt {20}}+4{\sqrt {45}}+{\sqrt {5}}+{\sqrt {7}}.} {\sqrt {20}}+4{\sqrt {45}}+{\sqrt {5}}+{\sqrt {7}}.To do this, you need to factor 20 {\displaystyle 20} 20 as 2 × 2 × 5 {\displaystyle 2\times 2\times 5} 2\times 2\times 5. You also need to factor 45 {\displaystyle 45} 45 as 3 × 3 × 5 {\displaystyle 3\times 3\times 5} 3\times 3\times 5. If a radicand is already a prime number, it does not need to be factored. For example, since 5 {\displaystyle 5} 5 and 7 {\displaystyle 7} 7 are already prime numbers, 5 {\displaystyle {\sqrt {5}}} {\sqrt {5}} and 7 {\displaystyle {\sqrt {7}}} {\sqrt {7}} do not need to be factored.
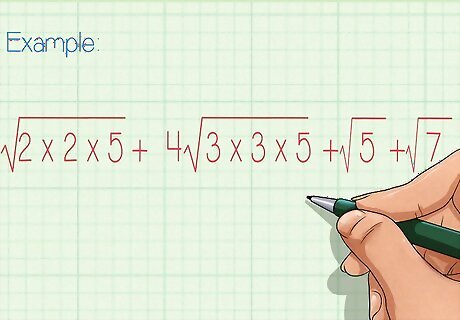
Rewrite the expression. Keep all the factors under the radical sign. For example, after factoring the radicands, the example expression would be 2 × 2 × 5 + 4 3 × 3 × 5 + 5 + 7 . {\displaystyle {\sqrt {2\times 2\times 5}}+4{\sqrt {3\times 3\times 5}}+{\sqrt {5}}+{\sqrt {7}}.} {\sqrt {2\times 2\times 5}}+4{\sqrt {3\times 3\times 5}}+{\sqrt {5}}+{\sqrt {7}}.
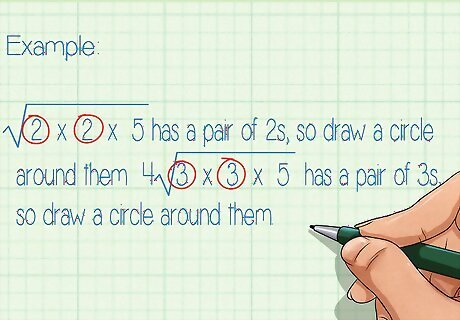
Circle pairs of like factors under each radical. Since you are finding a square root, by pairing up like factors, you can easily simplify the expression. For example, 2 × 2 × 5 {\displaystyle {\sqrt {2\times 2\times 5}}} {\sqrt {2\times 2\times 5}} has a pair of 2s, so draw a circle around them. 4 3 × 3 × 5 {\displaystyle 4{\sqrt {3\times 3\times 5}}} 4{\sqrt {3\times 3\times 5}} has a pair of 3s, so draw a circle around them.
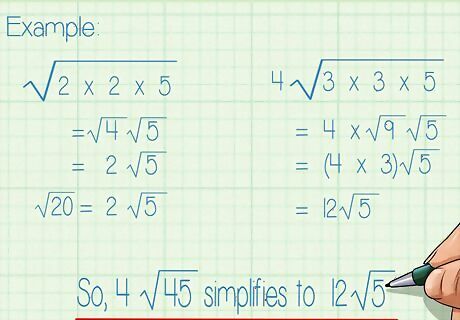
Factor out coefficients by identifying paired factors under each radical. The square root of any pair of factors will equal the factor, because x × x = x 2 {\displaystyle x\times x=x^{2}} x\times x=x^{{2}} and x 2 = x {\displaystyle {\sqrt {x^{2}}}=x} {\sqrt {x^{{2}}}}=x. Place this number in front of the radical sign. If the expression already has a coefficient, multiply the two numbers. For example: 2 × 2 × 5 {\displaystyle {\sqrt {2\times 2\times 5}}} {\sqrt {2\times 2\times 5}} = 4 5 {\displaystyle ={\sqrt {4}}{\sqrt {5}}} ={\sqrt {4}}{\sqrt {5}} = 2 5 {\displaystyle =2{\sqrt {5}}} =2{\sqrt {5}}So, 20 {\displaystyle {\sqrt {20}}} {\sqrt {20}} simplifies to 2 5 {\displaystyle 2{\sqrt {5}}} 2{\sqrt {5}}. 4 3 × 3 × 5 {\displaystyle 4{\sqrt {3\times 3\times 5}}} 4{\sqrt {3\times 3\times 5}} = 4 × 9 5 {\displaystyle =4\times {\sqrt {9}}{\sqrt {5}}} =4\times {\sqrt {9}}{\sqrt {5}} = ( 4 × 3 ) 5 {\displaystyle =(4\times 3){\sqrt {5}}} =(4\times 3){\sqrt {5}} = 12 5 {\displaystyle =12{\sqrt {5}}} =12{\sqrt {5}}So, 4 45 {\displaystyle 4{\sqrt {45}}} 4{\sqrt {45}} simplifies to 12 5 {\displaystyle 12{\sqrt {5}}} 12{\sqrt {5}}.
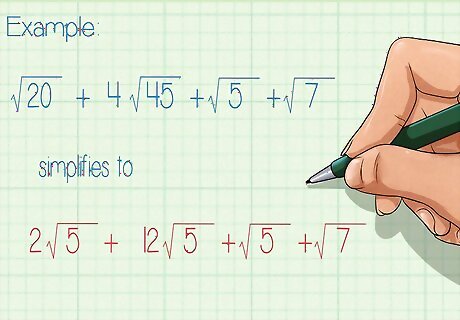
Rewrite your problem, using the simplified terms. This will make the adding process much easier. For example: 20 + 4 45 + 5 + 7 {\displaystyle {\sqrt {20}}+4{\sqrt {45}}+{\sqrt {5}}+{\sqrt {7}}} {\sqrt {20}}+4{\sqrt {45}}+{\sqrt {5}}+{\sqrt {7}} simplifies to 2 5 + 12 5 + 5 + 7 {\displaystyle 2{\sqrt {5}}+12{\sqrt {5}}+{\sqrt {5}}+{\sqrt {7}}} 2{\sqrt {5}}+12{\sqrt {5}}+{\sqrt {5}}+{\sqrt {7}}
Adding Square Roots
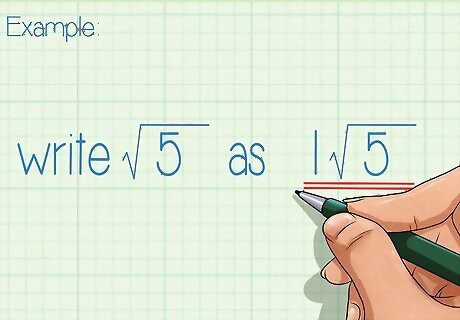
Place a 1 in front of any square root that doesn’t already have a coefficient. The 1 is always understood, and so is rarely written. However, when adding, writing the 1 can help you keep track of coefficients. A coefficient is the number in front of the radical sign. For example, write 5 {\displaystyle {\sqrt {5}}} {\sqrt {5}} as 1 5 {\displaystyle 1{\sqrt {5}}} 1{\sqrt {5}}.
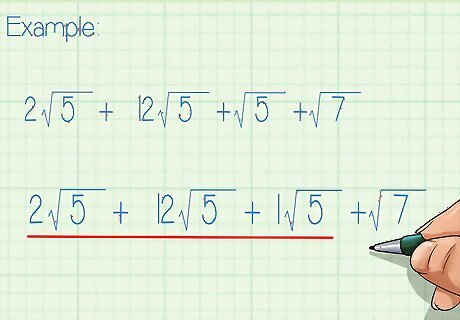
Check for square roots with the same radicand. You can only add square roots that have the same radicand. The radicand is the number underneath the radical sign. For example, you can add the first three terms in the expression 2 5 + 12 5 + 5 + 7 {\displaystyle 2{\sqrt {5}}+12{\sqrt {5}}+{\sqrt {5}}+{\sqrt {7}}} 2{\sqrt {5}}+12{\sqrt {5}}+{\sqrt {5}}+{\sqrt {7}}, because they all have the same radicand (5).

Add the coefficients. Only add the coefficients for terms that have the same radicand. Do NOT add the radicands. For example, 2 5 + 12 5 + 1 5 = 15 5 {\displaystyle 2{\sqrt {5}}+12{\sqrt {5}}+1{\sqrt {5}}=15{\sqrt {5}}} 2{\sqrt {5}}+12{\sqrt {5}}+1{\sqrt {5}}=15{\sqrt {5}}.
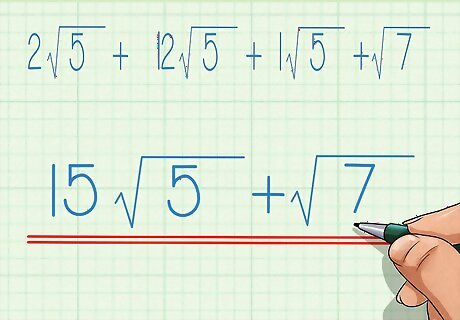
Add any unlike radicands to the expression. These cannot be simplified any further, and cannot be added to any other terms. The result will be your final, simplified answer. For example, 15 5 + 7 {\displaystyle 15{\sqrt {5}}+{\sqrt {7}}} 15{\sqrt {5}}+{\sqrt {7}}.


















Comments
0 comment